|
|
Quantum Hulls
-
Version
1.0
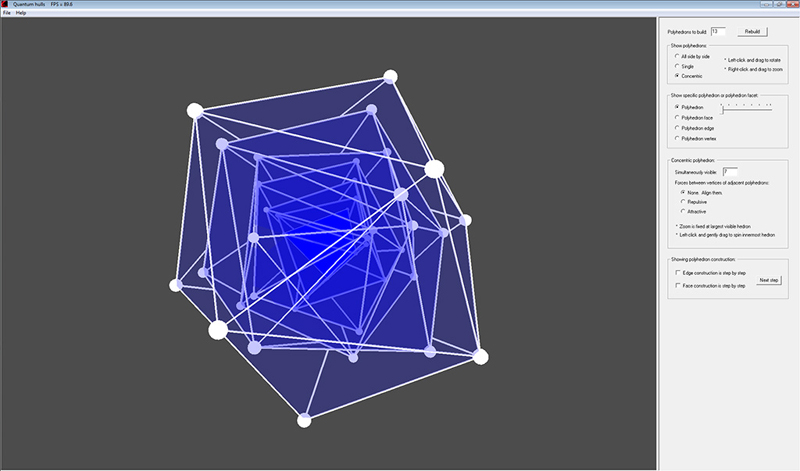
Visualization of the polyhedra whose vertices have
repelled eachother on the surface of a sphere, until
their positions have stabilized. The simplest such
polyhedron has 4 vertices, and naturally becomes a
tetrahedron. The remaining polyhedra, with an
integral number of vertices, are NOT regular
polyhedra. I call them "quantum hulls" because they
are all convex hulls with triangular faces, and the
number of vertices is quantized.
When the consecutive polyhedra are made to be
concentric, with the tetrahedron being the innermost
hull, and each hull is able to rotate freely about its
center, then it is interesting to see the dynamics
that occur when the vertices of each hull attract or
repel the vertices of the adjacent, outer concentric
hull. By rotating the innermost hull, all outer hulls
are affected in turn, and their orientations change to
find the lowest energy state, where the repulsive or
attractive forces are minimized.
|